Příklad 4
| > | f3:=(x^3-1)/(x^2-1); |
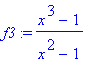
| > | plot(f3,x=-2..2,-6..6); |
![[Maple Plot]](image/spojitost_pr42.gif)
Body nespojitosti
| > | discont(f3,x); |
![]()
Vyšetřeme o jaký typ nespojitosti v jednotlivých bodech jde.
Bod x=-1
| > | Limit(f3,x=-1)=limit(f3,x=-1); |
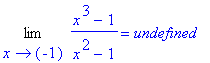
| > | Limit(f3,x=-1,left)=limit(f3,x=-1,left); |
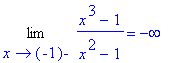
| > | Limit(f3,x=-1,right)=limit(f3,x=-1,right); |
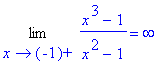
V bodě x=-1 je nespojitost druhého druhu.
Bod x=1
| > | Limit(f3,x=1)=limit(f3,x=1); |
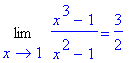
| > | Limit(f3,x=1,left)=limit(f3,x=1,left); |
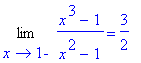
| > | Limit(f3,x=1,right)=limit(f3,x=1,right); |
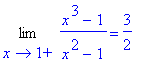
V bodě x=1 je odstranitelná singularita.
| > |