Příklad 1

Odstranitelná singularita  - problém při řešení rovnice

>	(x-1)^3/(x^2-1)=0;

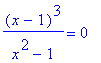
>	f:=lhs(%);

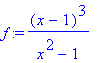
Řešíme rovnici pomocí

>	solve({f},x);

Vidíme, že řešením je bod x=1 , ale pokus o dosazení řešení selže, protože bychom dělili nulou. Poznamenejme, že tento příklad může být již systémem Maple spočten správně, neboť se systém velmi rychle vyvýjí.

>	subs(%,f);

Error, numeric exception: division by zero

Důvodem tohoto chování je odstranitelná singularita v bodě x=1 .

>	plot(f,x=-2..2,-8..8);

Nalezněme singulární body pomocí příkazů

>	discont(f,x);

>	singular(f);

Je vidět, že systém Maple v rámci příkazu singular  bod x=1  nepovažuje za singulární bod. Jediným možným vysvětlením je nalezení odstranitelné singularity v tomto bodě. To znamená, že zde existuje vlastní limita, pomocí níž Maple funkci dodefinoval. Právě zde je vidět závislost tohoto příkazu na příkazu solve .

>	Limit(f,x=1)=limit(f,x=1);

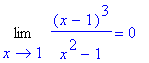
Tento příklad ukazuje důležitost znalosti singulárních bodů při práci s Maplem a hlavně uvádí pádný důvod pro provedení zkoušky dosazením při řešení rovnice pomocí příkazu solve .